3.2PROYECCIONES CABALLERAS
La perspectiva caballera es la proyección oblicua y cilíndrica (hecha con paralelas) de una figura. Para una buena comprensión de la figura la colocamos de forma que una cara esté paralela (x, z) o coincidente con el plano de cuadro o del dibujo. De esta manera la cara paralela mantiene sus dimensiones y forma inalteradas (homotecia afín), mientras que la proyección de su eje “y” experimenta una reducción (a / b) lo que favorece una apariencia más real de la figura.
Véase que la sombra de rayos paralelos (solar) de la figura con una cara paralela al suelo es la perspectiva caballera de la figura pero con ampliación del tamaño -en este caso por estar el sol en el crepúsculo- en vez de reducción como se viene utilizando en caballera. Las demás caras del cubo: verde, azul, violeta, esto es, las que no son paralelas al plano del cuadro, son afines a su representación o proyección en perspectiva caballera.
Perspectiva caballera del cubo
Aquí observamos la perspectiva caballera del cubo con una cara en verdadera forma y la profundidad del eje y reducido en este caso al 50%. El ángulo se empieza a contar a partir del eje x hacia la derecha, en este caso particular se ha escogido 315º sexagesimales. La pieza por encima de 180º se observa como si se estuviera viendo desde abajo.
La perspectiva caballera del cubo con una reducción de ¾ sobre el eje y (OA se reduce a OB en relación de 4 a 3).
Escalas de reducción: http://proporcion-escala-semejanza-homotecia.blogspot.com.es/
La perspectiva caballera de una recta m horizontal con sus 3 proyecciones m1 m2 m3.
La perspectiva caballera de una recta m horizontal con sus 3 proyecciones m1 m2 m3.
Tipos de rectas:
http://sistema-diedrico.blogspot.com.es/2010/11/elementos-punto-recta-y-plano.html
La perspectiva caballera de un plano oblicuo con sus 3 trazas p1 p2 p3.
Las trazas siempre se cortan en un eje, con lo que si nos dan p. ej., p1 y p3, basta con prolongar p1 hasta que corte al eje x, en el punto de intersección se pasa una recta por la intersección de p3-z y obtenemos p2.
La perspectiva caballera de un plano oblicuo con sus 3 trazas p1 p2 p3.
Las trazas siempre se cortan en un eje, con lo que si nos dan p. ej., p1 y p3, basta con prolongar p1 hasta que corte al eje x, en el punto de intersección se pasa una recta por la intersección de p3-z y obtenemos p2.
Tipos de planos:
http://sistema-diedrico.blogspot.com.es/2010/11/elementos-punto-recta-y-plano.html
Dos planos oblicuos z p en perspectiva caballera con su recta de intersección I.
Proyección del pentágono regular sobre el plano XOY con la reducción b/a sobre el eje y con un ángulo de 135º.
La perspectiva caballera de un cuadrado ABCD sobre el plano XOY con reducción ¾.
Paraboloide hiperbólico en perspectiva caballera.
Dos planos oblicuos z p en perspectiva caballera con su recta de intersección I.
Proyección del pentágono regular sobre el plano XOY con la reducción b/a sobre el eje y con un ángulo de 135º.
La perspectiva caballera de un cuadrado ABCD sobre el plano XOY con reducción ¾.
Paraboloide hiperbólico en perspectiva caballera.
La perspectiva caballera de un cilindro y un cono. El hecho de que la perspectiva caballera sea una proyección oblicua hace que las figuras salgan poco reales: el eje mayor de la elipse m (círculo en perspectiva) aparece con cierto ángulo respecto a la horizontal, cosa que no sucede en nuestra percepción visual que la reconoce siempre horizontal.
Consultar superficies radiadas:
http://sistema-diedrico.blogspot.com.es/2010/11/curvas-y-superficies.html
Pirámide con una cara apoyada en el plano YOZ. La longitud real del círculo de dimensión diametral OP, que inscribe la base de la figura, se reduce a la longitud OB.
BP determina por tanto la dirección de todos los puntos que se reducen sobre el eje y (AB).
La perspectiva caballera de un prisma recto de base hexagonal regular siguiendo los parámetros del ejercicio anterior.
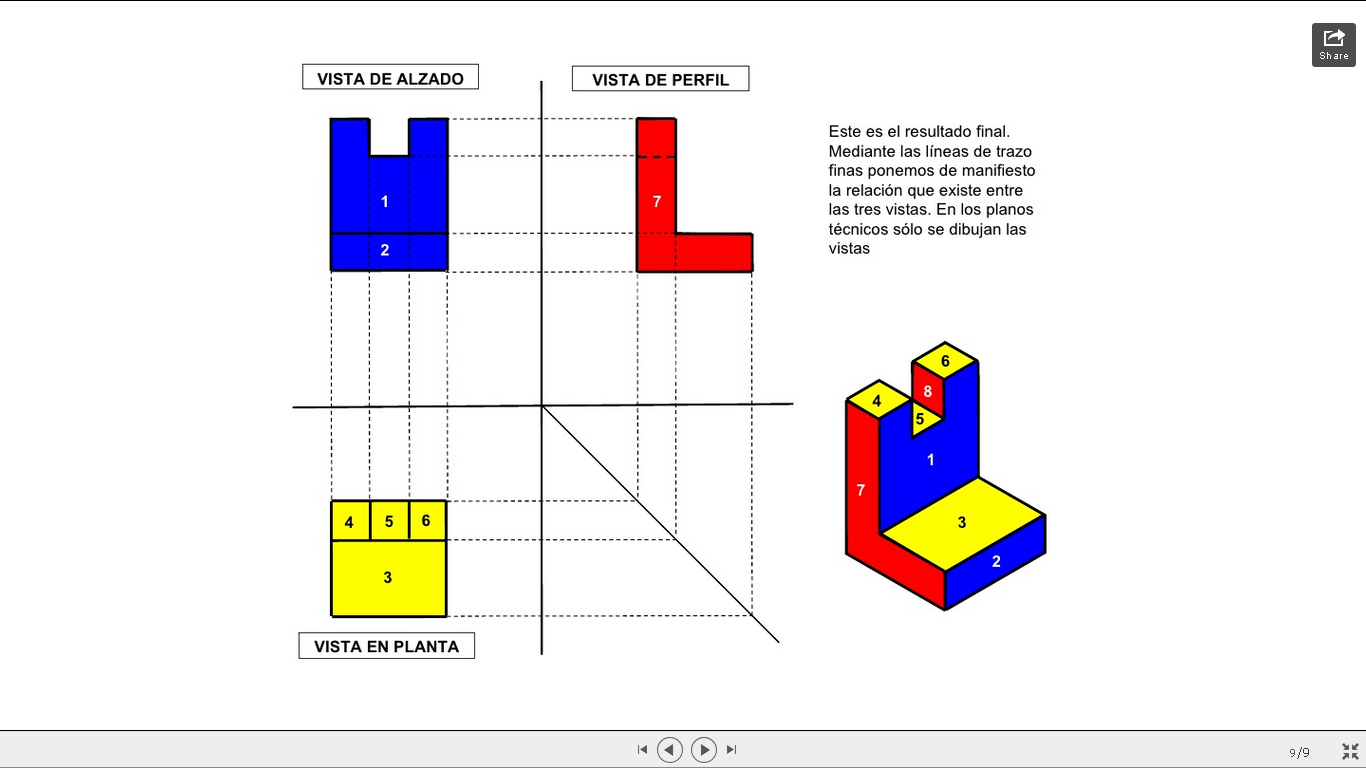
Pieza en perspectiva caballera construida a partir de sus proyecciones diédricas en planta y alzado. El segmento O2 se reduce a OA, longitud que se traslada al eje Z a la dimensión 1. (Por convenio la reducción se aplica sobre el eje y que es el que bascula, en el dibujo z y están intercambiados.)
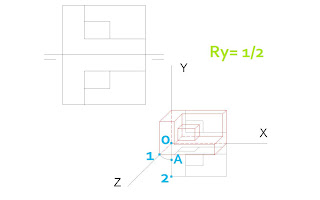
Pieza Con reducción ½. Para obtener la perspectiva de un punto cualquiera A, se proyecta su proyección A2 en la dirección del eje y A1 en la dirección de reducción 2 es a 1. La intersección de las dos direcciones A2-A y A1-A es la perspectiva del punto.
------------------------------------------------------------------------------
Superficies de revolución
Perspectiva cabellera de un toro (un donuts)
Construimos dos romboides que corresponden en perspectiva a dos cuadrados, en ellos inscribimos dos circunferencias que aparecen en la perspectiva como elipses verdes. Si giramos una de éstas elipses alrededor del eje de revolución K-L1, obtenemos la superficie amarilla que se llama toro.
Consultar la página de superficies de revolución:
http://sistema-diedrico.blogspot.com.es/2010/11/curvas-y-superficies.html
Una vez que hemos dibujado una de las elipses verdes, por ejemplo la de la izquierda, hacemos por el eje de revolución K-K1 líneas horizontales por distintos puntos (l1-K1-K-J1-L), preferentemente a distancias equidistantes, para que salga más homogénea la superficie.
Ésas líneas horizontales, de las que aparecen tres en el centro de color rojo y las tangentes a las elipses en color negro, cortan a las elipses en distintos puntos.
Por ejemplo la recta horizontal que corta al eje de revolución en K1, Corta a la elipse de la izquierda en los puntos D-C1.
Hacemos centro en K1 con un radio igual a K1-D, construyendo la circunferencia interior del toro. A continuación tomamos centro otra vez en K1 y tomando como radio K1-C1 hacemos una segunda circunferencia de revolución correspondiente a la parte exterior de la superficie.
Procedemos igual con las demás circunferencias, por ejemplo centro en K y radio Kl hacemos la circunferencia interior y centro en K y radio KI hacemos la circunferencia exterior.
El conjunto de todas las circunferencias tanto exteriores (las que están en la parte lateral de la superficie) como las interiores (correspondientes al hueco de la figura) definen la superficie y su contorno, que es la curva envolvente de todas estas circunferencias.
No se ha dibujado el contorno envolvente ya que el número de circunferencias dibujadas aproximan bastante el mismo.
Escocia
Escocia es la superficie de revolución que queda de un toro cuando sacamos su parte exterior, quedándonos exclusivamente con la zona que rodea al agujero. Por tanto la construcción está explicada en el ejercicio anterior, en el eje de revolución verde tomamos puntos que son los centros de las circunferencias cuyos diámetros horizontales interceptan en sus extremos a los puntos de las circunferencias en perspectiva, en este caso elipses de color magenta.
La parte exterior de la superficie se ha pintado en tonos amarillos y azules de forma alterna para que se distinga mejor, mientras que la parte interna aparece también pintada en color azul obscuro y naranja alternativamente.
Esfera
Para dibujar la esfera en perspectiva cabellera hacemos el meridiano o circunferencia mayor que pasa por el centro de la esfera T1 (como el Ecuador en la esfera terrestre), que por estar en el plano ADB aparece en el cuadrilátero ABCD en perspectiva oblicua con forma de romboide con una elipse verde inscrita.
A continuación dividimos el diámetro ON en partes iguales para que salgan los anillos equidistantes que definen la superficie y por cada uno de los puntos O-Q1-R1_S1, etc., hacemos rectas horizontales que interceptan a la elipse verde en puntos Z1-C!-A2, etc., que corresponden a los extremos de cada radio de la circunferencia que vamos a trazar tomando como centro los puntos descritos anteriormente sobre el eje de revolución ON.
Por ejemplo, por Q1 (centro) hacemos una circunferencia de radio Q1-Z1.
Por R1 (siguiente centro)hacemos otra circunferencia de radio R1-Z1. Se procede de igual forma con los demás puntos del eje de revolución.
El conjunto de todas las circunferencias delimitan un contorno también elíptico que define el contorno de la esfera, que en perspectiva caballera es siempre una elipse, ya que este sistema de representación es una proyección oblicua mediante paralelas y al proyectar de forma oblicua una esfera sobre un plano siempre se transforma en una elipse, por contraposición a la axonometría ortogonal, que proyecta perpendicularmente la esfera sobre un plano y por tanto su contorno es siempre una circunferencia.
La perspectiva caballera de una pirámide truncada de base cuadrada a reducción 3/5 y ángulo 45º. El ángulo en la perspectiva caballera siempre se toma en sentido de giro hacia la derecha y empezando a contar a partir del eje x.
La misma figura con una reducción de 2/3 y ángulo de reducción sobre el eje y de 2/3.
Si el punto A está localizado a cierta altura respecto al plano horizontal xy , una vez obtenida la perspectiva de su proyección A’ se levanta una vertical a partir de este punto con la cota en verdadera magnitud, que es la que corresponde al alzado en A2. La intersección de la dirección A-A2 (la del eje y) y de la vertical por A’ localiza al punto A.
La perspectiva caballera de dos prismas superpuestos con una reducción de 2/3 y ángulo de 135º. La longitud MO se reduce a PO sobre el eje y abatido, con lo que en la perspectiva M se transforma en P’. La dirección MP es la que define la reducción sobre el eje y y todos los puntos la siguen, así, N se transforma en N’, etc.
En la figura podemos observar la perspectiva caballera de un cilindro con sus dos proyecciones en planta y alzado, como el ángulo XOY’ es mayor de 180°, en este caso son 215°, la figura se ve como si la observáramos desde abajo. La reducción que se ha aplicado es de un medio.
En la prolongación del eje Z vemos como las dimensiones del cuadrado en planta se proyectan sobre el mismo generando el segmento a, a continuación este segmento se proyecta sobre el eje y’, con la reducción correspondiente. Podemos observar en la planta del cuadrado que por los vértices del mismo hemos hecho paralelas a estas direcciones -en color verde- para obtener sobre la cara XOY’ la proyección en perspectiva caballera de la planta.
En el dibujo observamos la forma de una casa en perspectiva caballera con el ángulo De 135° entre los dos ejes X e Y. El hecho de que la reducción sea ¾, sólo aplicable sobre el eje Y, supone que el segmento a aparece en el dibujo a ¾ de su dimensión real. Tenemos por contra que sobre los otros dos ejes, el horizontal y vertical, las medidas aparecen en verdadera magnitud, sin reducción alguna,- si el dibujo está hecho a escala uno partido uno.
En el dibujo observamos un cubo en perspectiva caballera con la reducción correspondiente y con un ángulo XOY’ de 135°. Se han calculado las sombras que proyecta sobre el suelo y las propias de la figura. Como los rayos del sol son paralelos, en color verde, estamos hablando de luz solar. Para ello se ha indicando la dirección norte-sur, como la dirección de la sombra del segmento vertical es n’, tenemos que el acimut es a, ya que es el ángulo que forma la dirección de la sombra de una vertical y la línea norte-sur hacia la derecha. Mientras que la altitud a la que está el sol, o sea el ángulo que forma respecto a la línea del horizonte es h.
http://calculo-de-sombras.blogspot.com/
http://calculo-de-reflejos.blogspot.com/
http://sombras-en-perspectiva-conica.blogspot.com/
http://reloj-de-sol.blogspot.com/
En el dibujo podemos observar la perspectiva caballera de una pirámide con un ángulo de 45°, como siempre contabilizado a partir del eje X y en el sentido de las agujas del reloj. Como podemos observar también el segmento b en planta correspondiente al lado de la base de la figura en color ocre se transforma en la perspectiva caballera en un segmento reducido a un medio, ya que hemos hecho centro en el origen de coordenadas de los ejes y trasladado el punto medio A mediante un giro sobre el eje y. La altura de la figura está en verdadera magnitud, ya que sobre el eje Z no se aplica reducción alguna.
La perspectiva militar es un caso particular de la perspectiva caballera en la que la planta de la figura es la que aparece en verdadera forma. Con ello podemos coger el plano de una casa y desplazarlo en una dirección vertical hasta obtener el techo o forjado del piso. Uniendo mediante líneas verticales las dos formas planas correspondientes al suelo y al techo obtenemos la perspectiva militar de la figura. El suelo y el techo de la casa están relacionados en una traslación u homotecia afín.
3. 3 PROYECCIONES AXONOMÉTRICAS
INTRODUCCION
La perspectiva axonométrica es un sistema de representación gráfica, consistente en representar elementos geométricos o volúmenes en un plano, mediante proyección paralela o cilíndrica, referida a tres ejes ortogonales, de tal forma que conserven sus proporciones en cada una de las tres direcciones del espacio: altura, anchura y longitud.
La perspectiva axonométrica cumple dos propiedades importantes que la distinguen de la perspectiva cónica:
- La escala del objeto representado no depende de su distancia al observador (equivalente a que el observador estuviera en el infinito).
- Dos líneas paralelas en la realidad son también paralelas en su representación axonométrica.
proporción de las medidas.
Cómo utilizarlo para el dibujo manual
Los ejes deben realizarse con escuadra, cartabón, goma, lápiz, regla, transportador . Marcaremos una línea vertical, llamada eje vertical y posteriormente los otros dos ejes, de anchura y longitud, con el ángulo que deseemos. Una vez realizados los ejes sólo quedará ir dibujando la pieza con las medidas dadas, aplicando los coeficientes reductores. El dibujo debe conservar la condición de paralelismo y proporcionalidad respecto de los tres ejes principales. También se utiliza para realizar los diseños previos llamados "a mano alzada", para ver si se puede realmente desarrollar la pieza, el espacio, el lugar u objeto que se va a proyectar. Se utiliza esta modalidad para obtener dibujos con medidas proporcionales.
TIPOS DE PERSPECTIVAS AXONOMETRICAS
|
Proyección axonométrica.
Se obtiene cuando el plano de proyección no es paralelo a ninguno de los tres ejes principales del objeto
 |
La proyección axonométrica, dependiendo
de los ángulos que forman entre sí los ejes axonométricos (proyecciones de los ejes principales
del objeto), se denomina
Perspectiva Isometrica
Se obtiene cuando los tres ángulos que forman los ejes axonométricos son iguales.
Al representar objetos en proyección isométrica se mide en una misma escala
sobre los tres ejes isométricos
Para la perspectiva axonométrica isométrica las profundidades se
trazan a 30 grados con las medidas reales, es decir, no sufre
acortamientos. Esta perspectiva es una técnica de representación
gráfica, es decir, que se representa el objeto tridimensional en dos
dimensiones, donde sus tres ejes coordenados ortogonales forman ángulos
iguales de 120º en el plano.
Este tipo de perspectiva es utilizada normalmente para realizar los
diseños previos. Su representación es neutral, fuera del espacio, en
donde las líneas del objeto quedan paralelas, acercando el objeto hacia
el espectador.
Este tipo de perspectiva es bastante utilizada por los
interioristas, ya que, esta modalidad nos permite dar dibujos con
medidas exactas a todo tipo de especialidades como los industriales. Además la
perspectiva isométrica tiene mucha aplicación en diseños arquitectónicos
y en el diseño industrial en donde se representan las piezas desde
variado puntos de vista.
Perspectiva Dimetrica
En la proyección Dimétrica se representa el ancho y la altura sin reducción y la
profundidad reducida a la mitad. Los ejes principales de la perspectiva forman
con la línea de referencia horizontal un ángulo de 7, 90, 42 grados respectivamente. Las aristas del cuerpo que discurren en profundidad aparecen muy reducidas.
Por motivos de simplificación, el ancho se redondea hasta 1, y la profundidad hasta 0.5. La dimetría según norma representa al objeto algo mayor de lo que es. Se aplica preferente cuando hay que dibujar algo esencial en la vista frontal. Se debe elegir como vista frontal la qué proporcione el máximo de datos sobreel objeto. La disposición de los ejes principales es de libre elección, para poder re-presentar la mayor cantidad posible de detalles. Es decir, el objeto puede ser proyectado en 7, 90, 42 o bien en 42, 90, 70.
Los ejes pueden dibujarse en varias posiciones, ya que cualquier objeto puede revelar sus detalles si se hace girar. Como es natural, la posición que se vaya a emplear, la determinará la posición que mostrará con más, claridad la totalidad de objeto o alguno de sus detalles en particular que no pueden observarse en alguna otra de sus vistas.
Proyección cindrica oblicua.
Se obtiene cuando la proyectantes no son perpendiculares al plano de proyección . Preferentemente al dibujar en proyección
oblicua se coloca el plano de proyección paralelo a una de las caras principales
del objeto; ya que de esta forma dicha cara se proyectará en verdadero tamaño
Al definir una proyección oblicua el eje recedente (eje de profundidad del objeto) se puede
proyectar formando cualquier ángulo (ao) con respecto a los otros dos; e independientemente
de este ángulo (ao), la profundidad
del objeto se puede proyectar también en cualquier longitud (teóricamente
hasta una longitud infinita).
Por lo tanto, al dibujar en proyección oblicua, se traza el eje recedente a cualquier ángulo, y se miden las profundidades sobre el en cualquier escala.
Perspectiva Caballera
La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.
Por lo tanto, al dibujar en proyección oblicua, se traza el eje recedente a cualquier ángulo, y se miden las profundidades sobre el en cualquier escala.
Perspectiva Caballera
La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.
En perspectiva caballera, dos dimensiones
del volumen a representar se proyectan en verdadera magnitud (el alto y
el ancho) y la tercera (la profundidad) con un coeficiente de
reducción. Las dos dimensiones sin distorsión angular con sus longitudes
a escala
son la anchura y altura (x, z) mientras que la dimensión que refleja la
profundidad (y) se reduce en una proporción determinada. 1:2, 2:3 o 3:4
suelen ser los coeficientes de reducción más habituales.
Los ejes X e Z forman un ángulo de 90º, y el eje Y
suele tener 45º (o 135º) respecto ambos.Se adoptan, por convención,
ángulos iguales o múltiplos de 30º y 45º, dejando de lado 90º, 180º,
270º y 360º por razones obvias.
Se puede dibujar fácilmente un volumen a partir de una vista lateral o alzado, trazando a partir de cada vértice líneas paralelas a Y, para reflejar la profundidad del volumen.
Este tipo de proyección es frecuentemente utilizada por su facilidad
de ejecución, aunque el resultado final no da una imagen tan real como
la que se obtendría con una proyección cónica.
Perspectiva Militar
La perspectiva militar es una proyección paralela oblicua, un sistema de representación por medio de tres ejes cartesianos (X, Y, Z).
En el dibujo, el eje Z es el vertical, mientras que los otros dos (X,
Y) forman 90° entre sí, determinando el plano horizontal (suelo).
Normalmente, el eje X se encuentra a 120° del eje Z, mientras que eje Y
se encuentra a 150° de dicho eje.
La principal ventaja radica en que las distancias en el plano horizontal conservan sus dimensiones y proporciones. Las circunferencias
en el plano horizontal se pueden trazar con compás, pues no presentan
deformación. Las circunferencias en los planos verticales se representan
como elipses.
3.3 PROYECCION CÓNICA CON DOS PUNTOS DE FUGA
